Mengapa `x^0` = 1 dan `x^-1` bisa terbalik menjadi `frac{1}{x}`?
Jawabannya bisa dikatakan sangat sederhana, yaitu kita harus mengetahui pengertian dari pangkat terlebih dahulu dan operasi-operasinya.
Pengurangan Eksponen
Untuk konsep pengurangan pangkat, maka bisa diartikan bahwa total bilangan yang dikalikan itu berkurang. Nah, untuk menguranginya kita menggunakan operasi pembagian, mengapa? Karena semisal kita punya `3^4` = 3`xx`3`xx`3`xx`3 untuk mengubahnya menjadi `3^3` tentunya kita tidak bisa menguranginya menjadi 3`xx`3`xx`3`xx`3 - 3 karena berdasarkan aturan operasi matematika yang mengharuskan kita untuk mengoperasikan perkalian dan pembagian terlebih dahulu dibanding pengurangan. 3`xx`3`xx`3`xx`3 - 3 malah akan menjadi `3^4 - 3`.
Itulah mengapa kita harus menggunakan operasi pembagian, sehingga kita bisa mengubah `frac{3xx3xx3xxcancel(3)}{cancel(3)}= frac{3^4}{3}= 3^(4-1) = 3^3`
Kesimpulannya, bentuk `(x^(y-1)) = frac{x^y}{x}`
Eksponen Nol
Kita sudah mendapatkan dasaran dari pengurangan eksponen di atas, di sini kita akan menerapkannya untuk membuktikan eksponen nol. Seperti yang bisa dilihat dari gambar bahwa eksponen nol kita definisikan sebagai suatu bilangan yang dibagi bilangan itu sendiri. Bisa kita tulis dengan `x^0 = x^(y-y) = frac{cancel(x^y)}{cancel(x^y)} = 1`
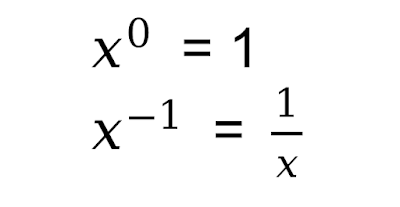

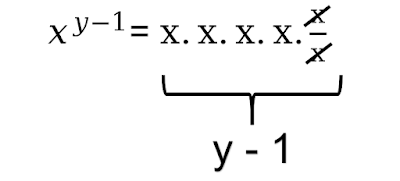


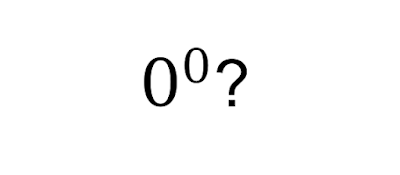

I love reading your blog. Your blog post is very useful and adds insight for me. Thank you for sharing.
BalasHapuspusing bacanya wkwkkw
BalasHapus