Pembuktian Aturan Cosinus

Daftar Isi

Sayang sekali jika aturan-aturan trigonometri hanya dihafal karena kegunaannya akan sangat sempit nantinya. Oleh karena itu, di sini saya akan membuktikan bagaimana rumus aturan cosinus tersebut bisa tercipta.

Untuk mencarinya, kita menggunakan konsep pythagoras, yaitu \(a^2 = b^2 + c^2\)

Mencari \(a^2\)

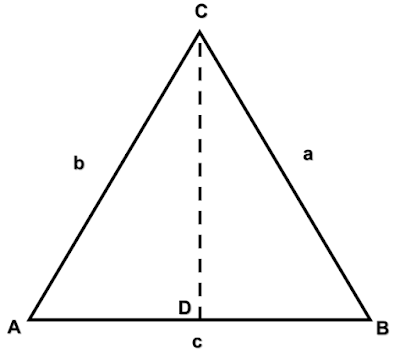
Kita menggunakan segitiga di atas sebagai dasarnya. Pertama-tama, mari kita cari sisi a.

\(a^2 = CD^2 + DB^2\)

Kita buat x = AD dan DB = c-x, maka

\(a^2 = (c-x)^2 + CD^2\)

\(CD = b.sinA\)

\(x = b.cosA\)

\(a^2 = (c-b.cosA)^2 + (b.sinA)^2\)

\(a^2 = c^2 -2cb.cosA + b^2.cos^2A + b^2.sin^2A\)

\(a^2 = c^2 -2cb.cosA + b^2(cos^2A + sin^2A)\)

Nah, di sini ada yang menarik.

Kita bisa mendapat identitas trigonometri untuk menyederhanakan persamaan di atas lagi-lagi menggunakan pythagoras

\(a^2 + b^2 = c^2`

\(\frac{a^2}{c^2} + \frac{b^2}{c^2} = \cancel{\frac{c^2}{c^2}}\)

\(\frac{a^2}{c^2} + \frac{b^2}{c^2} = 1\)

Jika \(\frac{a}{c} = sin\theta\) dan \(\frac{b}{c} = cos\theta\)

Maka `frac{a^2}{c^2}` = `frac{a}{c} xx frac{a}{c}` = sin`theta xx` sin`theta` = `sin^2theta` dan `frac{b^2}{c^2}` = `cos^2theta`

`sin^2theta + cos^2theta = 1`

Jadi, `a^2 = c^2 -2cb.cosA + b^2(1)`

`a^2 = c^2 -2cb.cosA + b^2`

`a^2 = c^2 + b^2 -2cb.cosA `

Mencari `b^2`

CD = a.sinB

x = a.cosB

`b^2 = (c-x)^2 + CD^2`

`b^2 = (c-a.cosB)^2 + (a.sinB)^2`

`b^2 = c^2 -2ca.cosB + a^2.cos^2B + a^2sin^2B`

`b^2 = c^2 -2ca.cosB + a^2(cos^2B + sin^2B)`

`b^2 = c^2 -2ca.cosB + a^2(1)`

`b^2 = c^2 -2ca.cosB + a^2`

`b^2 = c^2 + a^2 -2ca.cosB`

Mencari `c^2`

Untuk mencari `c^2` kita harus ganti garisnya. Tetapi ingat, garisnya harus bersudut 90°

AD = b.sinC

x = b.cosC

`c^2 = (a-x)^2 + AD^2`

`c^2 = (a-b.cosC)^2 + (b.sinC)^2`

`c^2 = a^2 -2ab.cosC + b^2.cos^C + b^2sin^2C`

`c^2 = a^2 -2ab.cosC + b^2(cos^C + sin^2C)`

`c^2 = a^2 -2ab.cosC + b^2(1)`

`c^2 = a^2 -2ab.cosC + b^2`

`c^2 = a^2 + b^2-2ab.cosC`

Kesimpulan

Dari uraian di atas, kita mendapatkan

`a^2 = c^2 + b^2 -2cb.cosA `

`b^2 = c^2 + a^2 -2ca.cosB`

`c^2 = a^2 + b^2-2ab.cosC`

Untuk memahami aturan cosinus tersebut secara sekilas, saya punya triknya.

Pertama, tentunya kalian harus melakukan visualisasi gambar segitiga di atas di pikiran kalian.

Idenya, kita hanya bisa menggunakan 1 sudut saja, agar identitas `sin^2theta + cos^2theta = 1` terpenuhi.

Setelah divisualisasikan, tentunya bentuknya adalah (contoh sisi a) `a^2 = (b.sinA)^2 + (c-b.cosA)^2`

Nah, di sini kalian langsung sederhanakan `(c-b.cosA)^2` terlebih dahulu, maka kesimpulan yang kita ambil adalah kita mendapatkan `c^2`, dan -2cb.cosA. Untuk sisanya tinggal coret saja cosA dan sinA karena nantinya akan berbentuk `cos^2A + sin^2A = 1` dan langsung saja bahwa hasilnya lainnya adalah `b^2`

Ya memang cukup ribet, karena hanya dijelaskan dengan kata-kata. Namun, jika kalian benar-benar memahaminya, hal tersebut akan sangat membantu. 

Matematika itu mamahami, bukan menghafal. Metode pemahamannya juga setiap orang berbeda-beda. Jadi, tidak ada salahnya jika kalian mempunyai metode khusus untuk memahami suatu aturan matematika, asalkan tidak menghafal.