Pembuktian Rumus Luas Segitiga Sama Sisi Tanpa Trigonometri

Dipublikasikan : Maret 22, 2021, Diperbarui : Maret 26, 2021

Pada kesempatan kali ini saya akan membahas pembuktian rumus luas yang cukup menarik, yaitu segitiga yang memiliki semua sisi yang sama. Biasanya sih materi ini berkaitan dengan ilmu Trigonomoteri, tapi di sini saya tidak akan mengaitkannya dengan ilmu tersebut. Namun, kalian sangat saya rekomendasi-kan untuk mempelajari Trigonometri karena ilmu ini berkaitan dengan perbandingan sisi persegi berdasarkan sudutnya.

Seperti biasa, kita potong dahulu segitiganya agar rapi dan mempermudah visualisasi.

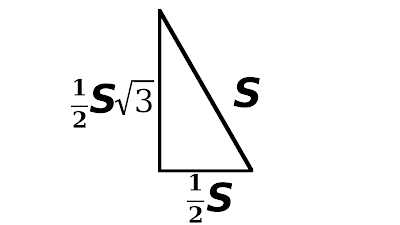
Nah, beginilah bentuk potongannya. Bangun ini merupakan segitiga siku-siku dan bisa diselesaikan dengan pythagoras untuk mencari sisi t. yaitu :

`t^2` = `s^2 - (frac{1}{2}s)^2`

`t` = `sqrt ( s^2 - (frac{1}{2}s)^2 :}`

`t` = `sqrt ( s^2 - frac{1}{4}s^2 :}`

`t` = `sqrt ( s^2 - frac{s^2}{4}:}`

`t` = `sqrt ( frac{4s^2 }{4}- frac{s^2}{4}:}`

`t` = `sqrt ( frac{3s^2}{4}:}`

`t` = `sqrt ( frac{1}{4}s^2xx3:}`

`t` = `frac{1}{2}s sqrt 3`

Dari sini kita sudah bisa menemukan bahwa tingginya adalah `frac{1}{2}s sqrt 3`

Nah, tadi kan kita memotong segitiga ini menjadi 2 bagian, maka bagian satunya kita susun di atas sehingga bangun segitiga siku-siku sekarang berubah bentuk mejadi persegi panjang. Tinggal kita kalikan saja sisi sisinya.

L = `frac{1}{2}s sqrt 3xxfrac{1}{2}s`

L = `frac{1}{2}xxfrac{1}{2}xxsxxsxxsqrt 3`

L = `frac{1}{4}s^2 sqrt 3`

Komentar

Postingan populer dari blog ini

Cara Menyalakan PSU ATX Tanpa Komputer Dengan Metode Jumper

Dipublikasikan : Agustus 16, 2020, Diperbarui : Juni 26, 2023

Halo semuanya. Mungkin sebagaian dari kalian bingung untuk menyalakan psu tanpa komputer atau hanya ingin mengetest psu saja tanpa harus memasangnya di motherboard komputer atau sebagainya. Teori PSU ATX akan hidup apabila sinyal pada PS-ON adalah low dan akan mati dalam keadaan standby apabila sinyal pada PS-ON high. Kondisi low didefinisikan sebagai kondisi di mana tegangan listrik berada pada kondisi minimum, yaitu 0V, sedangkan kondisi high berarti tegangannya berada pada nilai maksimumnya dalam kasus PS-ON ini adalah 5V. Pada kondisi awal, IC PWM yang membaca sinyal PS-ON akan dialiri tegangan 5V yang berarti dalam kondisi high sehingga membuat IC tersebut meresponnya dengan tidak mengaktifkan tegangannya. Apabila kita jumperkan kabel PS-ON yang berwarna hijau ke ground yang berwarna hitam, maka tentu saja tegangan pada PS-ON mengalir ke ground (negatif) sehingga PS-ON tidak mempunyai tegangan. Karena tidak ada tegangan, maka PS-ON akan didefinisikan dalam kondis

Baca selengkapnya

Menghilangkan Proteksi Pada Power Supply ATX LA8100PN Dan Sejenisnya

Dipublikasikan : Agustus 16, 2020, Diperbarui : Februari 19, 2024

Halo semuanya, pada tutorial kali ini saya ingin berbagi cara untuk menghilangkan sistem proteksi pada power supply atx atau biasa disebut juga psu komputer. Proteksi ini biasanya mencakup Over Current Protection, Over Voltage Protection, dan Under Voltage Protection. Nah, sistem proteksi-proteksi di atas akan menghalangi kalian untuk memakai seluruh daya pada psu atx, yang biasanya digunakan untuk MBR/Penghancur Short. Setelah sistem proteksi tersebut dihilangkan, maka kalian secara bebas dapat memakai seluruh daya pada psu tersebut, baik untuk MBR, Las Mini, dan bahkan untuk men-shortkannya pun tidak masalah (Sebentar saja). WARNING : DAPAT MENIMBULKAN KEBAKARAN JIKA TIDAK BERHATI-HATI DALAM MELAKUKAN LANGKAH-LANGKAHNYA. TANYAKAN KEPADA ORANG YANG BERKOMPETEN KETIKA INGIN MELAKUKAN PERCOBAAN LEBIH MENDALAM. Cara Mematikan Sistem Proteksi Ini adalah penampakan dari boardnya. Bagian yang saya lingkarin tersebut merupakan ic pwm dari psu ini.

Baca selengkapnya

Bisakah Kita Menggunakan HDD Komputer Di Laptop Atau Kebalikannya?

Dipublikasikan : Agustus 20, 2021, Diperbarui : Juni 24, 2023

Secara umum, hard disk memiliki dua jenis yang dibedakan berdasarkan ukurannya, yaitu hdd 2,5 inch dan hdd 3,5 inch. Bisa ditebak bahwa 2,5 inch digunakan pada laptop dan 3,5 inch pada komputer. Namun, apakah kita bisa membaliknya dengan menggunakan hdd laptop di komputer ataupun menggunakan hdd komputer di laptop? Jawabannya sangat bisa. Kabel pada hdd, dibagi menjadi dua dengan kedua fungsi yang berbeda, yaitu sebagai kabel tegangan (power sata) dan kabel data (sata). Pada dasarnya, semua hdd menggunakan port sata (bawah) dan kabel power hdd (atas) yang sama, baik itu pada jenis 2,5 inch dan 3,5 inch. Di atas adalah pin dari kabel sata sebagai kabel transportasi data. Semua kabel dan port sata pasti menggunakan konfigurasi seperti itu sehingga perpindahan data pada hard disk laptop dan komputer pada dasarnya sama saja. Hal ini memungkinkan untuk kedua tipe hard disk digunakan sebagai penyimpanan internal, baik di laptop maupun komputer. Perbedaannya terdapat pada kabel powernya. Hdd

Baca selengkapnya

Pembuktian Aturan Cosinus

Dipublikasikan : Juni 12, 2021, Diperbarui : September 24, 2023

Sayang sekali jika aturan-aturan trigonometri hanya dihafal karena kegunaannya akan sangat sempit nantinya. Oleh karena itu, di sini saya akan membuktikan bagaimana rumus aturan cosinus tersebut bisa tercipta. Untuk mencarinya, kita menggunakan konsep pythagoras, yaitu `a^2 = b^2 + c^2` Mencari `a^2` Kita menggunakan segitiga di atas sebagai dasarnya. Pertama-tama, mari kita cari sisi a. `a^2 ` = `CD^2` + `DB^2` Kita buat x = AD dan DB = c-x, maka `a^2 = (c-x)^2 + CD^2` CD = b.sinA x = b.cosA `a^2 = (c-b.cosA)^2 + (b.sinA)^2` `a^2 = c^2 -2cb.cosA + b^2.cos^2A + b^2.sin^2A` `a^2 = c^2 -2cb.cosA + b^2(cos^2A + sin^2A)` Nah, di sini ada yang menarik. Kita bisa mendapat identitas trigonometri untuk menyederhanakan persamaan di atas lagi-lagi menggunakan pythagoras `a^2 + b^2 = c^2` `frac{a^2}{c^2} + frac{b^2}{c^2} = cancel(frac{c^2}{c^2)}` `frac{a^2}{c^2} + frac{b^2}{c^2} = 1` Jika `frac{a}{c}` = sin`theta` dan `frac{b}{c}` = cos`theta` Maka `frac{a^2}{c^2}` = `frac{a}{c} xx frac{a}{c}`

Baca selengkapnya

Cara Clone Aplikasi Secara Tidak Terbatas Di Android

Dipublikasikan : Maret 11, 2020, Diperbarui : Agustus 26, 2020

Clone atau menggandakan aplikasi sudah menjadi hal lumrah saat ini. Pasalnya, hal tersebut sangat berguna ketimbang kita membeli handphone lain. Yuk! Simak tutorialnya di bawah ini. (H3) Cara Clone Aplikasi Di Android Pertama-tama silahkan install aplikasinya terlebih dahulu. Disini saya menggunakan aplikasi Multi Parallel - Multiple Accounts & App Clone yang bisa kalian download melalui link berikut https://play.google.com/store/apps/details?id=multi.parallel.dualspace.cloner Setelah diinstall, untuk clone aplikasi silahkan pencet Add Clone Lalu, pencet aplikasi yang ingin kalian clone. Nah, setelah kalian klik aplikasi yang kalian mau clone pasti terdapat centang birunya dan silahkan pencet Add Clone . Tulisan (1) adalah banyaknya aplikasi yang saya mau clone yaitu cuma 1 aplikasi. Maka aplikasi yang telah kalian clone akan terlihat di halaman depan dari aplikasi Multi Paralle

Baca selengkapnya

Memperbaiki Jalur Putus Pada Keyboard Dengan Conductive Ink DIY

Dipublikasikan : Februari 12, 2021, Diperbarui : Juli 08, 2023

Halo semuanya. Beberapa hari yang lalu keyboard membrane saya tidak berfungsi sebagian hurufnya dan memiliki pola yang teratur. Sayapun penasaran sehingga memutuskan untuk membongkarnya. Setelah dicek ternyata benar, yaitu terjadi putus di salah satu jalurnya. Ada beberapa pilihan untuk memperbaiki hal tersebut, seperti conductive ink ataupun copper tape. Namun, menurut saya conductive ink lebih gampang diatur penempatannya karena bentuknya adalah cairan encer hingga sedikit kental. Harga dari conductive ink juga tidak terlalu mahal sebenarnya, yaitu mulai dari Rp20.000,00 di toko kuning. Masalahnya adalah saya tinggal di Jawa Timur dan ongkirnya bisa-bisa seharga barangnya. Hal tersebut membuat saya malas untuk membelinya. Terlintaslah di pikiran saya untuk membuat conductive ink sendiri di rumah. Bahannya sederhana, hanya lem dan bubuk konduktif, seperti bubuk grafit. Lem yang digunakan bisa lem apapun yang mudah ditemukan di rumah dan memiliki karakteristik

Baca selengkapnya

Zahrayudha.ID

Search This Blog