Cara Membaca Boardview Di Linux

Daftar Isi

Halo. Mungkin Linux bisa dijadikan OS yang cocok bagi kalian para teknisi untuk membaca boardview dengan lebih mudah dikarenakan seperti yang kita tahu bahwa Linux tidak terlalu memakan banyak resource device kalian. 

Nah, pada tutorial ini saya akan menjelaskan bagaimana menginstall aplikasi pembaca boardview di Linux dengan menggunakan software OpenBoardView. Software tersebut saya pilih dikarenakan memiliki banyak kelebihan yaitu sebagai berikut:

• Bisa membaca format FZ (Memakai key), BRD, BRD2, BDV and BV* 
• Multi-platform, tidak hanya Linux, melainkan bisa dijalankan di Windows dan MacOS
• Gratis dan Open Source

Pertama-tama, kalian harus mempunyai wget pada sistem kalian (hampir semua distro sudah menyertakan ini). Kalau tidak punya, silahkan diinstall terlebih dahulu.  

 

Cara Install OpenBoardView di Debian dan Turunannya (Ubuntu)

Buka terminal dan ketikkan perintah berikut,

 

Untuk 64bit: 

wget https://github.com/OpenBoardView/OpenBoardView/releases/download/8.95.0/openboardview_8.95.0-1_amd64.deb -O openboardview64.deb && dpkg -i openboardview64.deb

Untuk 32bit:

wget https://github.com/OpenBoardView/OpenBoardView/releases/download/8.0/openboardview_8.0-1_i386.deb -O openboardview32.deb && dpkg -i openboardview32.deb

 

Cara Install OpenBoardView di Arch Linux dan Turunannya (Manjaro)

 Untuk Arch Linux punya cara yang lebih mudah karena sudah tersedia di AUR dengan nama openboardview-git.

Maka dari itu bisa langsung saja diinstall melalui AUR Helper. Jika tidak tahu atau mau build manual silahkan baca di sini. 

Untuk dari AUR bisa support 32bit dan 64bit, 

yay -S openboardview-git

 yay bisa diganti dengan AUR Helper yang ada di sistem kalian.

 

atau bisa juga cara lainnya (hanya 64bit),

wget https://github.com/utzlol/openboardview_arch/raw/main/openboardview-git-r665.e3a8179-1-x86_64.pkg.tar.zst -O  openboardview.pkg.tar.zst && sudo pacman -U openboardview.pkg.tar.zst

 

Cara Install OpenBoardView di Fedora dan Turunannya (CentOS)

Sayangnya pada Fedora, saya tidak bisa menemukan paket yang dalam versi 32bit. 

 

Untuk Fedora 64bit,

wget https://github.com/OpenBoardView/OpenBoardView/releases/download/8.0/openboardview-8.0-1.x86_64.rpm -O openboardview64.rpm &&  sudo rpm -i openboardview64.rpm

  

 

Penyelesaian Masalah Error Saat Membuka File .FZ

openboardview: /home/yudha/.cache/yay/openboardview-git/src/openboardview-git/src/openboardview/FileFormats/FZFile.cpp:234: FZFile::FZFile(std::vector<char>&, uint32_t*): Assertion `content != nullptr' failed.

 Aborted (core dumped) 

 

Masalah ini sering (selalu) terjadi saat kita pertama kali install OpenBoardView dan tidak jarang membuat sebagaian user bingung. Tapi tenang, sebenarnya masalah ini dapat diatasi dengan mudah, yaitu dengan memasukkan FZ Key.

FZ key dapat kalian copy dari sini atau copy text di bawah,

0x25d8d248  0xe1502405  0x56b5d486  0x69213fe0  0xa22490ec  0x01fdd9fa  0x0681955f  0x0fac202d  0xdac9eeb4  0xf6024aba  0xcd8b4cc6  0x9f307c8e  0x4ab8fad7  0x232f967d  0x5e8666a3  0xde966d4b  0xc64bfb1c  0xea7fb092  0x1a751a7e  0x37e8f0bc  0x3359c8f3  0x969ac22b  0x610f5804  0xd99d10e6  0xc58d54d6  0x1f9aea8b  0x8e388c1a  0xe4f7d2ed  0x3e5da1f6  0xedfe818a  0x7252b016  0xb503a170  0xc4128fb6  0x2c93ceeb  0x53539a6e  0xdacf7668  0x3ab78e52  0x8ee9d815  0x7043f799  0xc6a05dcf  0x727f1da2  0x0dfd983b  0x78c53872  0x00945692 

  

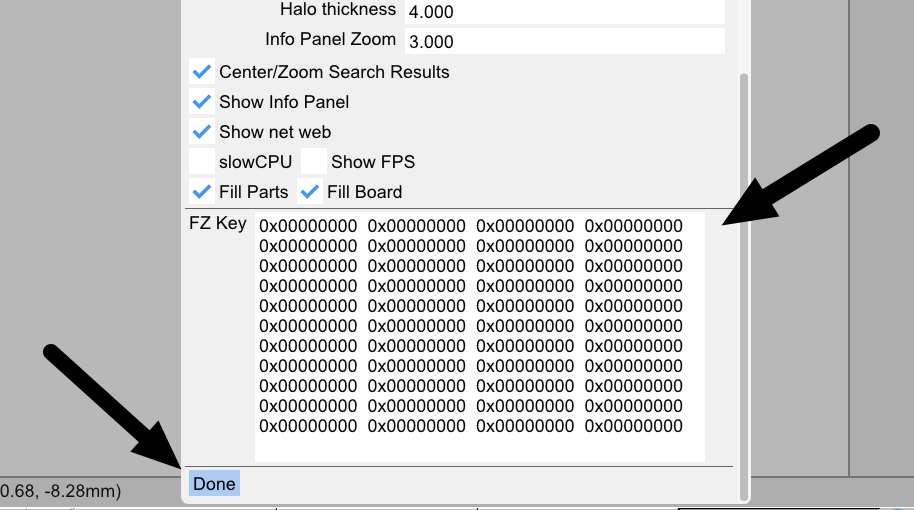
Setelah dicopy, kalian buka OpenBoardView dan klik menu File --> Program Preferences

 

Lalu paste textnya di kolom FZ Key dan klik Done.

 

Kalau kalian kembali ke menu sebelumnya. Maka, penampakannya akan seperti ini (FZ Keynya terisi).
 

 

Sip! kita telah berhasil untuk membuka .FZ file dengan OpenBoardView.

 

Terima kasih. Jika menemui kendala, silahkan berkomentar.